Menu
Substance
A summary of Penrose's summary of physics and math.
"The beauty and power of complex analysis, such as with the above-mentioned property whereby solutions of the 2D Laplace equation - an equation of considerable physical importance - can be very simply represented in terms of holomorphic functions, led 19th-century mathematicians to seek 'generalized complex numbers,' which could apply in a natural way to 3D space." (pg. 198)
William Rowan Hamilton discovered the following in 1843: \[i^2 = j^2 = k^2 = ijk = -1\] (i, j, k are bolded - say my notes, and therefore probs vectors)
where each of \(i\), \(j\), and \(k\) are an independent 'square root of -1' \(\bullet\) a quaternion ...
3 Blue 1 Brown - Visualizing quaternions (4d numbers) with stereographic projection
-Quaternions and 3d rotation, explained interactively
\[q = t + ui + vj + wk\] with \(t\), \(u\), \(v\), \(w\) real
\(\bullet\) quaternions are not commutative! (\(ab \neq ba\)) \(\bullet\) properties: ---1. commutative addition \(a + b = b + a\) ---2. associative addition \(a + (b + c) = (a + b) + c\) ---3. associative multiplication \(a(bc) = (ab)c\) ---4. distributive laws \((a(b+c) = ac + ab\) and \((a+b)c = ac + bc\) ---5. additive identity \(a+0 = a\) ---6. multiplicative identity \(|a + a| = a\) The properties numbered 1-5 meet the requirements for this to be an algebraic ring while the 6th property further allows for the classification as a ring with identity. \(\bullet\) quaternions form a 4-dimensional vector space over the real numbers since they have 4 independent basis quantities \l\), \(i\), \(j\), \(k\) spanning the space of quanternion \(\bullet\) due to the multiplication law, they provide an algebra over the real numbers \(\bullet\) they also have the structure of a division ring since they have multiplicative inverses: \[q^{-1}q = qq^{-1} = 1\] \[q^{-1} = \bar{q}(q\bar{q})^{-1}\] where the latter is the explicit definition of the inverse. \(\bullet\) the conjugate is defined as \[\bar{q} = t - ui - vj - wk\] \(\bullet\) \(q\bar{q} = t^{2} + u^{2} + v^{2} + w^{2}\) which is a real, nonzero number unless \(q = 0\) \(\bullet\) quaternions have not proven to be very useful in physics, for example \(q\bar{q}\) does not have the correct signature (I suppose he is referring to the Minkowski signature) for use in relativity \(\bullet\) cannot define quaternion-holomorphic functions because \(\bar{q}\) would have to be such a function of \(q\) and we previously defined holomorphic functions as those of the complex variable \(z\), independent of \(\bar{z}\) Geometry of Quaternions
Let \(i\), \(j\), \(k\) be three orthogonal axes in Euclidean space. Then, multiplying \(i\) is a rotation about the \(i\) axis with the \((j, k)\)-plane as the complex place and likewise for \(j\) and \(k\). In order to satisfy the properties of quaternions however, rather than rotating 90\(^{\circ}\) as before, we must now rotate by 180\(^{\circ}\)/\(\pi\) radians. An important property occurs when rotating by \(2\pi\), we find that \(i^{2} = 2\) rather than \(-1\). \(\star\) This yields the notion of a spinor! \(\star\) That is, "an object with turns into its negative when it undergoes a complete rotation through \(2\pi\)" (pg. 204). Thus, the number of \(2\pi\) rotations have a parity based on if they are even or odd. "To picture a spinoral object, we can think of an ordinary object in space, but where there is an imaginary flexible attachment to some fixed external structure..." (pg. 205).
Clifford Algebras
\(\bullet\) to discuss higher dimensions, must consider what the analogue of a rotation is about an axis is in n dimensions, such a rotation is about an "axis" that is an \(n-2)\) dimensional space.
---- in higher dimensions, a composition of rotations about an \((n-2)\) dimensional axis is not always a rotation about an \((n-2)\) dimensional axis \(\bullet\) more simple to first consider reflections about an \((n-1)\) dimensional hyperplane where a composition of 2 such reflections wrt. 2 hyperplanes constitutes a \(\pi\) rotation (so can consider such reflections as secondary entities) \(\bullet\) let \(\gamma_{1}\). \(\gamma_{2}\), \(\gamma_{3}\), ... , \(\gamma_{n}\) be reflections where \(\gamma_{r}\) reverses the \(r^{th}\) coordinate axis there are \(n\) quaternion-like relations: \(\gamma_{1}^{2} = -1\), \(\gamma_{2}^{2}= -1\), \(\gamma_{3}^{2} = -1\), ..., \(\gamma_{n}^{2} = -1\) then the \(\pi\)-rotation entities are products of \(\gamma_{i}\)'s with the anticommutation property: \(\gamma_{p}\gamma_{q} = -\gamma_{q}\gamma_{p}\) with \(p \neq q\). (So for 3D, can express \(i = \gamma_{2}\gamma_{3}\), \(j = \gamma_{3}\gamma_{1}\), \(k = \gamma_{1}\gamma_{2}\).) \(\bullet\) General element of a Clifford algebra for \(n\) dimensional space is a linear combination of products of distinct \(\gamma\)'s 1st order = the \(n\) \(\gamma_{i}\)'s 2nd order = the \(\frac{1}{2}n(n-1)\) independent products \(\gamma_{p}\gamma_{q}\) (with \(p < q\) 3rd order = the \(\frac{1}{6}n(n-1)(n-2)\) 3 \(\gamma\) products ...and so on The sum of "entities" is thus \[1 + n + \frac{1}{2}n(n-1) + \frac{1}{6}n(n-1)(n-2) + ... + 1 = 2^{n}\] This is a sum of \(n\) choose \(k\) for \(k\) from 0 to \(n\). \(\bullet\) The Clifford algebra is therefore a \(2^{n}\)-dimensional algebra over the reals ---- a ring with identify ---- unlike quaternions though, they are not a division ring "A spinor may be thought of as an object upon which the elements of the Clifford algebra act as operators" (pg. 210). \(\bullet\) the spin space (space of spinors) in \(n\) dimensions: ---- for odd \(n\): \(2^{(n-1)/2}\) dimensional ---- for even \(n\): \(2^{n/2}\) dimensional...this splits into 2 spaces of reduced or half spinors of \(2^{(n-2)/2}\) dimensions each. So each element of the full spinor has a component from each of these subspaces. \(\bullet\) For even \(n\)-dimensional space, a reflection converts one half-spinor into the other. \(\bullet\) Elements of reduced spin space have a chirality (as do those of the opposite space with opposite chirality). Grassmann Algebras
\(\bullet\) Have anticommuting elements \(\eta_{1}, \eta_{2}, ..., \eta_{n}\) where each \(\eta_{i}\) squares to 0:
\(\eta_{1}^{2} = 0\), \(\eta_{2}^{2} = 0\), ..., \(\eta_{n}^{2} = 0\) \(\bullet\) Still have \(\eta_{p}\eta_{q} = -\eta_{q}\eta_{p}\) BUT can have \(p = q\) \(\bullet\) Unlike Clifford algebras, does not require there to be a metric on the space \(\bullet\) Can think of each \(\eta_{i}\) as a line element/vector associated to one of the \(n\) coordinate axis (Interesting note: the axes do not need to be orthogonal) \(\bullet\) Let us ahve 2 vectors at the origin: \[a = a_{1}\eta_{1} + a_{2}\eta_{2} + ... + a_{n}\eta_{n}\] \[b = b_{1}\eta_{1} + b_{2}\eta_{2} + ... + b_{n}\eta_{n}\] and denote the Grassmann/wedge product as \(a \wedge b\) \(\bullet\) we can find that \(a\wedge b = -b\wedge a\) \(\bullet\) \(a \wedge b\) = the plane element spanned by the two vectors \(\bullet\) We find the coefficients/components of \(a \wedge b\) to be the quantities \(a[_{p}b_{q}]\) with the square brackets denoting antisymmetrization. Antisymmetrization is defined generally by \[A_{[pq]} = \frac{1}{2}(A_{pq}-A_{qp})\] or more specifically here, \[a[_{p}b_{q}] = \frac{1}{2}(a_{p}b_{q} - a_{q}b_{p})\] \(\bullet\) \(a \wedge b \wedge c\) can then be thought of as a 3D plane element having an orientation and magnitude as before. One finds anticommutation properties: \[a \wedge b \wedge c = b \wedge c \wedge a = c \wedge a \wedge b = -b\wedge a \wedge c = -a\wedge c \wedge b = -c\wedge b \wedge a\] Notice how the odd permutations have a negative sign and the even ones do not. \(\bullet\) Grassmann algebra is a graded algebra ---- contains \(r^{th}\)-order elements with \(r\) the number of \(\eta\)'s that are wedge-producted togehter within the expression ---- the number \(r\) can range from 1 to \(n\) and is called the grade of the element of the Grassmann algebra Note: a general element of the algebra of grade \(r\) with \(r = 3\) for example, can be a sum of expressions of the form \(a \wedge b \wedge c\) For \(P\) an element of grade \(p\) and \(Q\) and element of grade \(q\), their \((p+q)\)-grade wedge product \(P\wedge Q\) has components \(P[_{a...c}Q_{d...f}]\) where \(P_{a..c}\) and \(Q_{d..f}\) are the components of \(P\) and \(Q\), respectively. \[P \wedge Q = \begin{cases}+Q\wedge P & p\textrm{, or } q\textrm{, or both are even}\\ -Q\wedge P & p\textrm{ and }q\textrm{ are both odd} \\ \end{cases}\] \(\star\star\star\) Should not confuse grade with degree of the form though I think they can be the same...idk, unsure at time of typing. "We may also add together elements of different grades to obtain a 'mixed' quantity that does not have any particular grade" (pg. 215). ...To which I wrote WHY?
0 Comments
The complex conjugate of \(z = x+iy\) is \(\bar{z}=x-iy\)
\(\bullet\) in the complex \(z\)-plane this operation constitutes a reflection of the plane in the real line By including the complex conjugate, we can get \(x\) and \(y\) by: \[x = \frac{z+\bar{z}}{2}\] \[y = \frac{z-\bar{z}}{2i}\] we can then express functions \(f(x, y)\) as \(F(z, \bar{z})\). These are 2-real-dimensional and non-holomorphic. Suppose you have a 2D surface \(S\) and a smooth function \(\Phi\) defined on \(S\). \(\Phi\) can then be a smooth map from \(S\) to \(\mathbb{R}\) or \(\mathbb{C}\). \(\bullet\) such a \(\Phi\) may be called a scalar field on \(S\) \(\bullet\) for \(\Phi = f(x, y)\) to be smooth, it must have both the derivatives wrt. \(x\) and \(y\) to be continuous functions of the coordinate pair \((x, y)\) \(\bullet\) for \(C^{1}\)-smoothness \(\frac{\partial f}{\partial x}\) and \(\frac{\partial f}{\partial y}\) must be continuous \(\bullet\) for \(C^{2}\)-smoothness \(\frac{\partial^{2}f}{\partial x^{2}}\), \(\frac{\partial^{2}f}{\partial y^{2}}\) and \(\frac{\partial^{2}f}{\partial x\partial y}\) must be continuous \(\bullet\) for \(C^{3}\)-smoothness: \[\frac{\partial^{3}f}{\partial x^{3}}\] \[\frac{\partial^{3}f}{\partial y^{3}}\] \[\frac{\partial^{3}f}{\partial x^{2}\partial y} = \frac{\partial^{3}f}{\partial x \partial y \partial x} = \frac{\partial^{3}f}{\partial y\partial x^{2}}\] and presumably \(\frac{\partial^{3}f}{\partial x\partial y^{2}}\) must all be continuous \(\bullet\) should we have a second set of coordinates on which \(\Phi\) acts, we have also \(\Phi = F(X, Y)\) "On an overlap region between the two patches, we shall therefore have \(f(x, y) = F(X, Y)\)." (pg. 185) \(X\) and \(Y\) in this case could be fucntions of \(x\) and \(y\). These are called transition fucntions: \[X = X(x, y) ... Y = Y(x, y)\] \[x = x(X, Y) ... y = y(X, Y)\] \(\bullet\) when the transition functions are smooth, the smoothness of \(\Phi\) is independent of the choice of coordinates on the overlapping region Vector Fields and 1-Forms
"There is a notion of 'derivative' of a function that is independent of the coordinate choice." (pg. 185)
\(\bullet\) for function \(\Phi\) defined on a 2-manifold surface \(S\), it is denoted \(d\Phi\) (which is a 1-form) \[d\Phi = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy\] in "disembodied operator form" this is \(d = dx\frac{\partial}{\partial x} + dy\frac{\partial}{\partial y}\) which arises from the chain rule. The operator \(\frac{\partial}{\partial x}\) which acts on the fucntion \(\Phi\) defined on the 2-manifold \(S\) can be given meaning through the chain rule which can relate differentiation of the variables \(X\) and \(Y\) to \(x\) as \[\frac{\partial}{\partial x} = \frac{\partial X}{\partial x}\frac{\partial}{\partial X} + \frac{\partial Y}{\partial x}\frac{\partial}{\partial Y}\] \(\bullet\) a vector field on \(S\) in the \((X, Y)\)-coordinate patch is defined as \[\mathcal{E} = A\frac{\partial}{\partial X} + B\frac{\partial}{\partial Y}\] where \(A\) and \(B\) are shown above.
In the \((x, y)\)-coordinate patch (or system) we have similarly \[\mathcal{E} = a\frac{\partial}{\partial x}+b\frac{\partial}{\partial y}\] can think of this as the gradient of \(\Phi\) \(\star\) note that even if \(X = x\), \(\frac{\partial}{\partial x} \neq \frac{\partial}{\partial X}\) since there is also a dependence on the other coordinate \(\bullet\) \(d\Phi\) = gradient/ exterior derivative of \(\Phi\) ---can be used to obtain contour lines on \(S\) ---\(\frac{\partial}{\partial x}\) points along lines of constant \(y\) ---\(\frac{\partial}{\partial y}\) points along lines of constant \(x\) \(a\) and \(b\) can be used to label \(\mathcal{E}\), referred to as its components in the \((x, y)\) system (or coordinate labels) \(\bullet\) \(d\Phi = udx + vdy\) where \(u\) and \(v\) are components of \(d\Phi\) in \((x, y)\) system \(\bullet\) \((u, v)\) of \(d\Phi\) (the 1-form) and \((a, b)\) of \(\mathcal{E}\) (the vector field) are related by the scalar or inner product (\(\mathcal{E}(\Phi)\) or \(d\Phi\bullet\mathcal{E}\): \[\mathcal{E}(\Phi) = d\Phi\bullet\mathcal{E} = au + bv = a\frac{\partial\Phi}{\partial x} + b\frac{\partial\Phi}{\partial y}\] \(\bullet\) a 1-form is also called a covector \(\bullet\) 1-forms are dual to vector fields \(\bullet\) contour lines occur where \(d\Phi\bullet\mathcal{E} = 0\) The Cauchy-Riemann Equations
How to characterize the complex-valued functions \(\Phi\) which are holomorphic?
\(\bullet\) on (\(x\), \(y\)), \(\Phi\) must be holomorphic in \(z = x + iy\) \(\bullet\) on (\(X\), \(Y\)), \(\Phi\) must be holomorphic in \(z = X + iY\) \(\bullet\) \(Z\) must be a holomorphic function of \(z\) where the coordinate systems overlap in \(S\) Suppose we can express \(\Phi\) as a function of \(z\) and \(\bar{z}\) and that \(\Phi\) is independent of \(\bar{z}\), that is \(\frac{\partial\Phi}{\partial\bar{z}} = 0\), then \(\Phi\) is holomorphic. By the chain rule, this is equivalent to \(\frac{\partial\Phi}{\partial x} + i\frac{\partial\Phi}{\partial y} = 0\). Writing \(\Phi = \alpha + i\beta\) we can get \(\frac{\partial\alpha}{\partial z} = \frac{\partial\beta}{\partial y}\) and \(\frac{\partial\alpha}{\partial y}=-\frac{\partial\beta}{\partial x}\), the Cauchy-Riemann equations. Then we must also have \[\frac{\partial X}{\partial x} = \frac{\partial Y}{\partial y}\] and \[\frac{\partial X}{\partial y} = -\frac{\partial Y}{\partial x}\] when this holds for any (\(x\), \(y\)) and (\(X\), \(Y\)) we have a Riemann surface \(S\). When \(\alpha\) and \(\beta\) satisfy \(\frac{\partial\alpha}{\partial x} = \frac{\partial\beta}{\partial y}\) and \(\frac{\partial\alpha}{\partial y} = -\frac{\partial\beta}{\partial x}\) then Laplace's equations are satisfied \[\nabla^{2}\alpha = 0 ... \nabla^{2}\beta = 0\] the 2-dimensional Laplacian is defined \[\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}\] Laplace's equation in 3D plays fundamental role in \(\bullet\) Newtonian gravity: equation satisfied by potential function determining the gravitational field \(\bullet\) electrostatics: equation satisfied by the potential function determining the static electric field (both in free space) \(\star\) solutions to the Cauchy-Riemann equations can be derived from solutions to teh 2D Lapalce equation if \(\alpha\) satisfies \(\nabla^{2}\alpha=0\), then we get \(\beta\) from \(\beta = \int\frac{\partial\alpha}{\partial x}dy\)
\(\bullet\) Fourier analysis = procedure for studying waveforms originally intended for the purpose of decomposing periodic vibrations into their "sine-wave" parts
\(\bullet\) a function \(f(x)\) with \(x\) a real number is periodic if \(f(x+l) = f(x)\) for some fixed period \(l\) \[\sin{x + 2\pi} = \sin{x}\] \[\cos{x + 2\pi} = \cos{x}\] arising from periodicity of \(e^{ix}=\cos{x}+i\sin{x}\). Note that \(e^{i(x+2\pi)}=e^{ix}\). \(\bullet\) to get period \(l\) we use \(e^{i 2\pi x/l)}\) instead of \(e^{ix}\) \(\bullet\) \(e^{i 2\pi nx/l}\), \(\sin{\frac{2\pi nx}{l}}\), \(\cos{\frac{2\pi nx}{l}}\) represent a higher "nth" harmonic that oscillates \(n\) times in the period \(l\) \(\bullet\) the decomposition of \(f(x)\) into its "pure tones" \[f(x) = c + a_{1}\cos{wx} + b_{1}\sin{wx} + a_{2}\cos{2wx} + b_{2}\sin{2wx} + a_{3}\cos{3wx} + b_{3}\sin{3wx} + ...\] where \(w = 2\pi/l\) (the angular frequency). Alternatively, \[f(x) = ... + \alpha_{-2}e^{-2iwx}+\alpha_{-1}e^{-iwx}+\alpha_{0}+\alpha_{1}e^{iwx}+...\] where \(a_{n}=\alpha_{n}+\alpha_{-n}\) and \(b_{n}=i\alpha_{n}-i\alpha_{-n}\) and \(c=\alpha_{0}\) for \(n = 1, 2, 3, ...\) \(\bullet\) letting \(z=e^{iwx}\) we get \[F(x) = ... + \alpha_{-2}z^{-2} + \alpha_{-1}z^{-1} + \alpha_{0}z^{0} + \alpha_{1}z^{1} + \alpha_{2}z^{2} + ...\] So we have \[F(z) = \sum\alpha_{r}z^{r}\] (a Laurent series) where \(F(z) = F(e^{iwx}) = f(x)\) \(\bullet\) annulus of convergence (of a Laurent series) is the region strictly between two circles in the complex plane both centered at the origin Suppose \(F^{-} = \alpha_{1}z^{1}+\alpha_{2}z^{2}+\alpha_{3}z^{3}+...\) has a circle of convergence with radius \(A\) (so \(F^{-}\) converges for all \(z\) with modulus \(< A\)) \[F^{+} = ...+\alpha_{-3}z^{-3}+\alpha_{-2}z^{-2}+\alpha_{-1}z^{-1}\] can be written in terms of \(w=\frac{1}{z}\) as \[F^{+} = ... + \alpha_{-3}w^{3}+\alpha_{-2}w^{2}+\alpha_{-1}w^{1}\] Suppose \(F^{+}\) has a circle of convergence in the \(w\) plane with radius \(\frac{1}{B}\) st. it converges for all \(w\) with modulus \(< \frac{1}{B}\), or alternatively for all \(z\) with modulus \(> B\). So when \(B < A\), we have the annulus of convergence \(\bullet\) for \(f(x)\) analytic, convergence of \(F(z)\) requires the unit circle on which \(z\) lays to be within the annulus of convergence \(\bullet\) for \(f(x)\) that is not analytic, the unit circle ends up on the boundary of what should be an open region Frequency Splitting
\(F^{+}(z)\) is holomorphic in the southern hemisphere, positive-frequency part
\(F^{-}(z)\) is holomorphic in the northern hemisphere, negative-frequency part Note: standard orientation of unit circle in \(z\)-plane is direction of increase of the \(\theta\)-coordinate (anti clockwise). For a loop, orientation is anticlockwise if clock face is on inside of loop and vice versa.
When dealing with time, we can define future and past limits as \(t = \infty\) and \(t = -\infty\) and \(x\) limits from \(\pi\) to (-\pi\). This means that \(z=e^{ix}\) goes around the unit circle in an anticlockwise direction starting and finishing at \(z=-1\). Then we can define \[t = \tan{\frac{1}{2}x}\] Then we have the transformations between the \(z\)-plane and real number time plane given by \[t = \frac{z-1}{iz+1}\] \[z = \frac{-t+i}{t+i}\] For \(p\) (ex. a momentum) and \(x\) (a position) and a large period (ie. \(l = 2\pi N\) with \(N \mapsto \infty\)) we have \[f(x) = (2\pi)^{-\frac{1}{2}}\int_{-\infty}^{\infty}g(p)e^{ixp}dp\] \[g(p) = (2\pi)^{-\frac{1}{2}}\int_{-\infty}^{\infty}f(x)e^{-ixp}dx\] \(f(x)\) and \(g(p)\) are Fourier transforms of eachother
\(\bullet\) a complex \(f(x)\) defined on the real line has positive freqeuncy if \(g(p) = 0\) for all \(p \geq 0\)
\(\bullet\) Riemann Surface:
- \(\log{z}\) is the simplest - \(z^{a}\) with a rational number - \(z^{a}\) with an irrational number is same as \(\log{z}\) - for \(z^{a}\) with \(a\) a rational number with "lowest terms expression" \(a=m/n\), sheets of the Riemann surface join after \(n\) terms \(\bullet\) Branch Point: the origin \(z = 0\) in the examples above \(\bullet\) for the example of \(z^{a}\) with \(a = m/n\), the branch point is of finite order/order \(n\) \(\bullet\) else (as for \(\log{z}\)), the branch point has infinite order. \((1-z^{3})^{1/2}\) has 3 branch points \[z = 1\] \[z = w\] \[z = w^{2}\] with \(w = e^{2\pi i/3}\). At each of these points then, \(1-z^{3} = 0\). There is also another branch point at \(z = \infty\). Circling around a branch point locally, causes the function to change sign after the first rotation and return to its starting value after the second. This gives the branch points order 2. \(\bullet\) the Riemann surface is a torus with 4 tiny holes corresponding to the branch points \(\star\) Riemann Surface = general notion of a manifold looks like Euclidean space locally "Manifolds may be thought of as being glued together from a number of different patches, where the gluing job really is seamless." (pg. 138) \(\bullet\) conformal geometry deals with shapes on the infinitesimal scale \(\bullet\) conformal maps preserve infinitesimal shapes only alternatively, "angles between curves are preserved in a conformal transformation" (pg. 140) \(\bullet\) the holomorphicity of a function implies that the mapping is conformal and non-reflective/orientation preserving Examples: \[w = az + b\] \[w = z\] \(\bullet\) inversion = holomorphic transformation followed by a reflection in the real axis \(\bullet\) bilinear/ Mobius transformation \[w = \frac{az+b}{cz+d}\] The Riemann Sphere
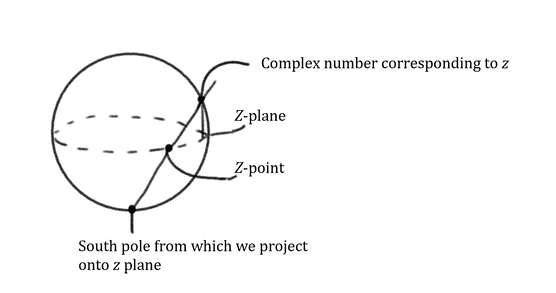
\(\bullet\) constructed from 2 "coordinate patches"; the z-plane and the w-plane (both complex planes)
\(\bullet\) only 2 points have either a \(z\) or \(w\) coordinate but not both \(\bullet\) can define them as \(w = \frac{1}{z}\) and \(z = \frac{1}{w}\) with \(z = 0 \mapsto w = \infty\) and \(w = 0 \mapsto z = \infty\) \(\bullet\) Consider the \(z\) complex plane and the equatorial plane of the sphere. Points of the sphere are mapped to this plane via stereographic projection
The same is done from the north pole with the w plane also at the equator but "upside down" or mirrored.
\(\bullet\) Riemann sphere = simplest compact/closed Riemann surface \(\bullet\) "spiral ramp" surface of \(\log{z}\) is non-compact \(\bullet\) for \((1-z^{3})^{1/2}\), need to fill in the 4 holes to make it compact ("compactification") The Genus of a Compact Riemann Surface
\(\bullet\) genus = number of branches or holes or loops
----sphere has genus 0 ----torus has genus 1 ----pretzel has genus 3 \(\bullet\) there is only one complex modulus \(p\) for genus 1, for genus 2, there are 3 \(\bullet\) generally, the number \(m\) of complex moduli for genus \(g\) where \(g \geq 2\) is \(m = 3g - 3\) \(\bullet\) for \(g \geq 2\) there are no holomorphic/continuous self-transformations of the Riemann surfaces but there are discrete ones \(\bullet\) for \(g = 1\) the transformations (really translation) can be achieved by \(z \mapsto z + a\) with the single parameter \(a\) \(\bullet\) for \(g = 0\) the transformations are given by the bilinear transformations \[z \mapsto \frac{az+b}{cz+d}\] Let \(s\) be the number of complex parameters required to specify a self transformation, then we have \(s = 0\) for \(g \geq 2\) \(s = 1\) for \(g = 1\) \(s = 3\) for \(g = 0\)
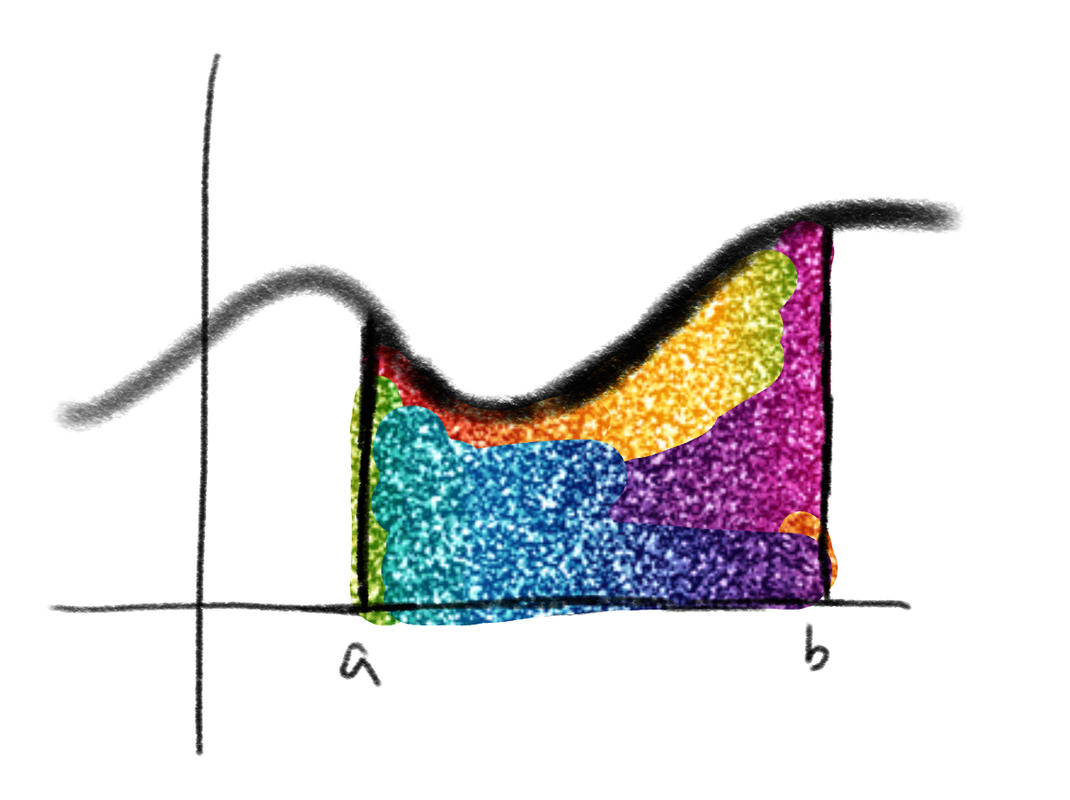
Consider the function \(f(x)\) where \(z\) is a complex number. The definite integral on complex variable \(z\): \[\int_{a}^{b}f(z)dz = g(b) - g(a)\] \(\bullet\) there are multiple paths from \(a\) to \(b\) when we are on a complex plane
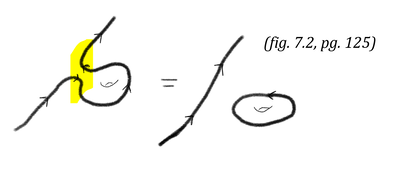
\(\bullet\) the answer would be the same along all such paths which can be obtained via continuous deformation of the original \(\star\) results from "fundamental theorem of exterior calculus" If a function has an undefined value, then this yields a hole on the complex plane which means that there may exist multiple integration paths which cannot be related via continuous deformation. \(\bullet\) these continuous deformations are called "homologous deformations" \(\bullet\) paths related by homologous deformations are in the same "homology class" \(\bullet\) homologous deformations can have orientations that cancel when a path loops
Consider \(f(z) = \frac{1}{z}\) with a complex variable. The definite integral is given by \[\int_{a}^{b}\frac{dz}{z} = \log{b} - \log{a}\] where \(a\) and \(b \in \mathbb{C}\). Recall that the logarithm of a complex value can be expressed as the logarithm of a real value and \(i\theta\). That is, we can express \[\log{b} = \log{r} + i\theta\] \[\log{a} = \log{s} + i\phi\] Varying only one of the complex numbers above, we can see that we can increase the phase (\(\theta\)) of the integral by \(2\pi\) with each positive rotation about the origin of the path of integration.
Closed Contours
As described above, one can visualize closed contour integration graphically by:
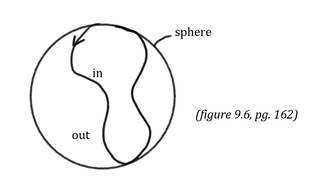
\(\bullet\) varying the 2nd path first \(\bullet\) then varying the first path in the reverse direction (since it is being subtracted) \(\bullet\) cancelling out alternate orientation portions The loop/closed path to the right below is called a contour
\(\star\) the contour is independent of the location of \(a\) and \(b\)
This gives us the notion of a closed contour integral \[\oint \frac{dz}{z} = 2\pi i\] For a holomorphic function \(f(z)\), its value at the origin is given by the Cauchy formula as \[\frac{1}{2\pi i} \oint \frac{f(z)}{z}dz = f(0)\] the left is essentially any loop around the origin \(\bullet\) the nth derivative \(f^{n}(0)\) can be obtained from \[\frac{n!}{2\pi i}\oint\frac{f(z)(z^{n+1}}dz = f^{n}(0)\] \(\bullet\) more generally, about any point \(p\) we have \[\frac{1}{2\pi i}\oint\frac{f(z)}{z-p}dz = f(p)\] \[\frac{n!}{2\pi i}\oint\frac{f(z)}{(z-p)^{n+1}}dz=f^{n}(p)\] "Complex smoothness implies analytcity (holomorphicity) at every point of the domain." (pg. 128) Using these variations of Cauchy formulas, we can write a power series about any point in an open, complex-smooth region. Further, this power series will be convergent. \(\bullet\) singular point = singularity of \(f(z)\) for \(z\) complex \(\bullet\) regular point = point at which \(f(z)\) does not have a singularity/ where it is holomorphic Singular and regular points are covered at the start of the Differential Topology text.
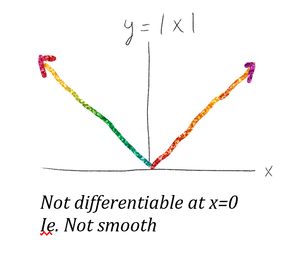
Thinking of functions as maps allows us to define non-smooth functions as well as those pieced together from other functions like:
\[\theta(x) = \frac{|x|- x}{2x}\] ie. the Heaviside Step Function C^n-smoothness
\(f(x) = x^{n}|x|\) with \(n\) a positive integer is \(C^{n}\)-smooth because it can only be differentiated to a smooth function n times.
Now consider \(h(x)=\begin{cases}0 & x\leq 0\\ e^{-1/x} & x > 0 \\ \end{cases}\) which is \(\bullet\) \(C^{\infty}\)-smooth over \(\mathbb{R}\) \(\bullet\) can think of as 2 functions glued together Sticking to real number functions, let the power series of \(f(x)\) be \[f(x) = a_{0} + a_{1}x + a_{2}x^{2} + a_{3}x^{3} + a_{4}x^{4} + ...\] To have an expansion in this form, \(f(x)\) must be \(C^{\infty}\)-smooth so that one may differentiate \(f(x)\) infinitely to obtain an approximation of the terms of the expansion which are of course infinite. analytic functions
In \(h(x)\), the coefficients of the Maclauren series at the origin \(x = 0\), ie. \(a_{n} = f^{n}(0)/n!\) are all zero on both sides. Thus, \(h(x)\) is NOT analytic at the origin. You cannot gain any information about \(h(x)\) from its expansion about the origin.
However, a power series about some other point is given by \[f(x) = a_{0} + a_{1}(x-p) + a_{2}(x-p)^{2} + a_{3}(x-p)^{3} + ...\] with \(a_{n} = f^{n}(p)/n!\). For some \(x\) infinitesimally close to \(p\) st. we can essentially say \(x=p\), if the values of \(a_{n}\) give more information than before (ie. are not always zero at p), then the function is called analytic. \(\bullet\) analytic/\(C^{\infty}\)-smooth function = analytic at all \(p\) in its domain Differentiation Rules
\[\frac{d(x^{n})}{dx} = nx^{n-1}\] \[d[f(x) + g(x)] = df(x) + dg(x)\] \[d{af(x)} = adf(x)\] for \(a\) a constant
the "Leibniz Law": \[d\{f(x)g(x)\} = f(x)dg(x) + g(x)df(x)\] \[d\{f(g(x))\} = f'(g(x))g'(x)dx\] \[d\left(\frac{f(x)}{g(x)}\right) = \frac{g(x)df(x) - f(x)dg(x)}{g(x)^{2}}\] Integration
Other Notes:
- Penrose refers to \(C^{n}\) as the differentiability class, ie. functions that can be differentiated n times
-defines the Heaviside step function \(\theta(x)\) as a \(C^{-1}\) function and the Dirac delta function (its derivative) as a \(C^{-2}\) function |
Archives
April 2022
Categories |
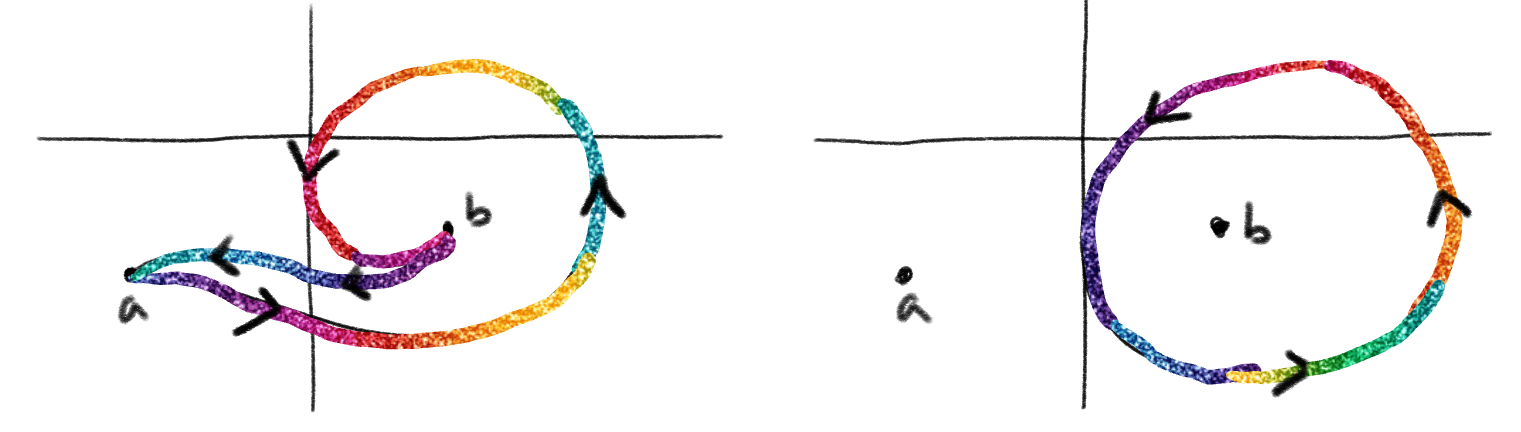
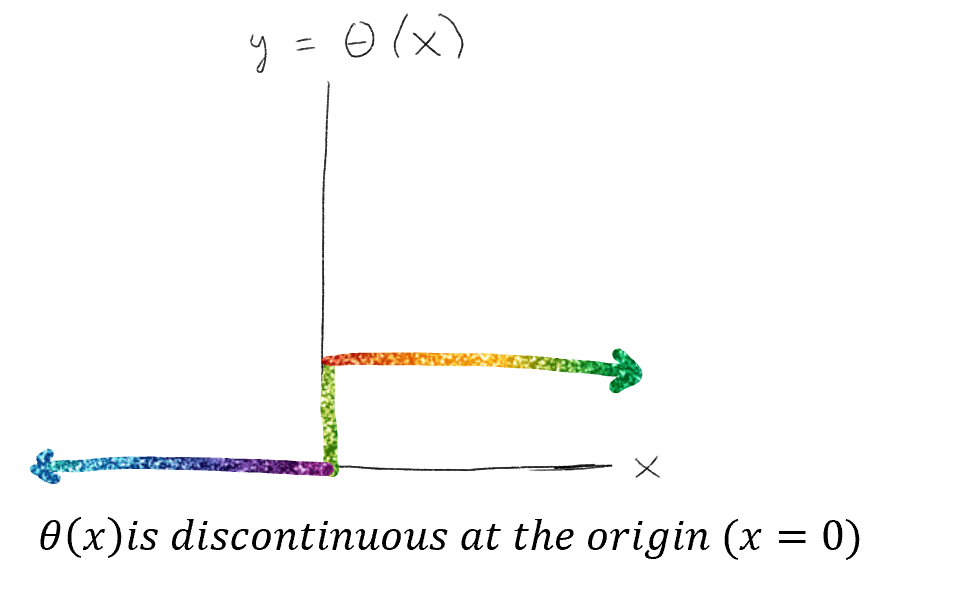
 RSS Feed
RSS Feed