Chapter 8: Riemann Surfaces and Complex Mappings

\(\bullet\) Riemann Surface:
- \(\log{z}\) is the simplest
- \(z^{a}\) with a rational number
- \(z^{a}\) with an irrational number is same as \(\log{z}\)
- for \(z^{a}\) with \(a\) a rational number with "lowest terms expression" \(a=m/n\), sheets of the Riemann surface join after \(n\) terms

\(\bullet\) Branch Point: the origin \(z = 0\) in the examples above
\(\bullet\) for the example of \(z^{a}\) with \(a = m/n\), the branch point is of finite order/order \(n\)
\(\bullet\) else (as for \(\log{z}\)), the branch point has infinite order. \((1-z^{3})^{1/2}\) has 3 branch points \[z = 1\] \[z = w\] \[z = w^{2}\] with \(w = e^{2\pi i/3}\). At each of these points then, \(1-z^{3} = 0\). There is also another branch point at \(z = \infty\). Circling around a branch point locally, causes the function to change sign after the first rotation and return to its starting value after the second. This gives the branch points order 2.
\(\bullet\) the Riemann surface is a torus with 4 tiny holes corresponding to the branch points

\(\star\) Riemann Surface = general notion of a manifold looks like Euclidean space locally

"Manifolds may be thought of as being glued together from a number of different patches, where the gluing job really is seamless." (pg. 138)

\(\bullet\) conformal geometry deals with shapes on the infinitesimal scale
\(\bullet\) conformal maps preserve infinitesimal shapes only alternatively, "angles between curves are preserved in a conformal transformation" (pg. 140)
\(\bullet\) the holomorphicity of a function implies that the mapping is conformal and non-reflective/orientation preserving
Examples: \[w = az + b\] \[w = z\]
\(\bullet\) inversion = holomorphic transformation followed by a reflection in the real axis
\(\bullet\) bilinear/ Mobius transformation \[w = \frac{az+b}{cz+d}\]

The Riemann Sphere

\(\bullet\) constructed from 2 "coordinate patches"; the z-plane and the w-plane (both complex planes)
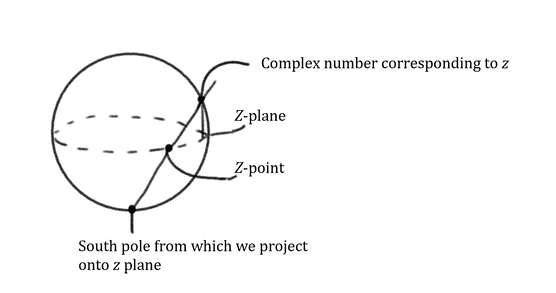
\(\bullet\) only 2 points have either a \(z\) or \(w\) coordinate but not both
\(\bullet\) can define them as \(w = \frac{1}{z}\) and \(z = \frac{1}{w}\) with \(z = 0 \mapsto w = \infty\) and \(w = 0 \mapsto z = \infty\)
\(\bullet\) Consider the \(z\) complex plane and the equatorial plane of the sphere. Points of the sphere are mapped to this plane via stereographic projection

The same is done from the north pole with the w plane also at the equator but "upside down" or mirrored.

\(\bullet\) Riemann sphere = simplest compact/closed Riemann surface
\(\bullet\) "spiral ramp" surface of \(\log{z}\) is non-compact
\(\bullet\) for \((1-z^{3})^{1/2}\), need to fill in the 4 holes to make it compact ("compactification")

The Genus of a Compact Riemann Surface

\(\bullet\) genus = number of branches or holes or loops
----sphere has genus 0
----torus has genus 1
----pretzel has genus 3
\(\bullet\) there is only one complex modulus \(p\) for genus 1, for genus 2, there are 3
\(\bullet\) generally, the number \(m\) of complex moduli for genus \(g\) where \(g \geq 2\) is \(m = 3g - 3\)
\(\bullet\) for \(g \geq 2\) there are no holomorphic/continuous self-transformations of the Riemann surfaces but there are discrete ones
\(\bullet\) for \(g = 1\) the transformations (really translation) can be achieved by \(z \mapsto z + a\) with the single parameter \(a\)
\(\bullet\) for \(g = 0\) the transformations are given by the bilinear transformations \[z \mapsto \frac{az+b}{cz+d}\]

Let \(s\) be the number of complex parameters required to specify a self transformation, then we have
\(s = 0\) for \(g \geq 2\)
\(s = 1\) for \(g = 1\)
\(s = 3\) for \(g = 0\)