Menu
Substance
A summary of Penrose's summary of physics and math.
|
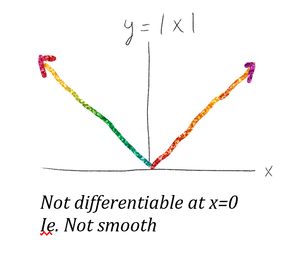
Thinking of functions as maps allows us to define non-smooth functions as well as those pieced together from other functions like:
\[\theta(x) = \frac{|x|- x}{2x}\] ie. the Heaviside Step Function C^n-smoothness
\(f(x) = x^{n}|x|\) with \(n\) a positive integer is \(C^{n}\)-smooth because it can only be differentiated to a smooth function n times.
Now consider \(h(x)=\begin{cases}0 & x\leq 0\\ e^{-1/x} & x > 0 \\ \end{cases}\) which is \(\bullet\) \(C^{\infty}\)-smooth over \(\mathbb{R}\) \(\bullet\) can think of as 2 functions glued together Sticking to real number functions, let the power series of \(f(x)\) be \[f(x) = a_{0} + a_{1}x + a_{2}x^{2} + a_{3}x^{3} + a_{4}x^{4} + ...\] To have an expansion in this form, \(f(x)\) must be \(C^{\infty}\)-smooth so that one may differentiate \(f(x)\) infinitely to obtain an approximation of the terms of the expansion which are of course infinite. analytic functions
In \(h(x)\), the coefficients of the Maclauren series at the origin \(x = 0\), ie. \(a_{n} = f^{n}(0)/n!\) are all zero on both sides. Thus, \(h(x)\) is NOT analytic at the origin. You cannot gain any information about \(h(x)\) from its expansion about the origin.
However, a power series about some other point is given by \[f(x) = a_{0} + a_{1}(x-p) + a_{2}(x-p)^{2} + a_{3}(x-p)^{3} + ...\] with \(a_{n} = f^{n}(p)/n!\). For some \(x\) infinitesimally close to \(p\) st. we can essentially say \(x=p\), if the values of \(a_{n}\) give more information than before (ie. are not always zero at p), then the function is called analytic. \(\bullet\) analytic/\(C^{\infty}\)-smooth function = analytic at all \(p\) in its domain Differentiation Rules
\[\frac{d(x^{n})}{dx} = nx^{n-1}\] \[d[f(x) + g(x)] = df(x) + dg(x)\] \[d{af(x)} = adf(x)\] for \(a\) a constant
the "Leibniz Law": \[d\{f(x)g(x)\} = f(x)dg(x) + g(x)df(x)\] \[d\{f(g(x))\} = f'(g(x))g'(x)dx\] \[d\left(\frac{f(x)}{g(x)}\right) = \frac{g(x)df(x) - f(x)dg(x)}{g(x)^{2}}\] Integration
Other Notes:
- Penrose refers to \(C^{n}\) as the differentiability class, ie. functions that can be differentiated n times
-defines the Heaviside step function \(\theta(x)\) as a \(C^{-1}\) function and the Dirac delta function (its derivative) as a \(C^{-2}\) function
0 Comments
Leave a Reply. |
Archives
April 2022
Categories |
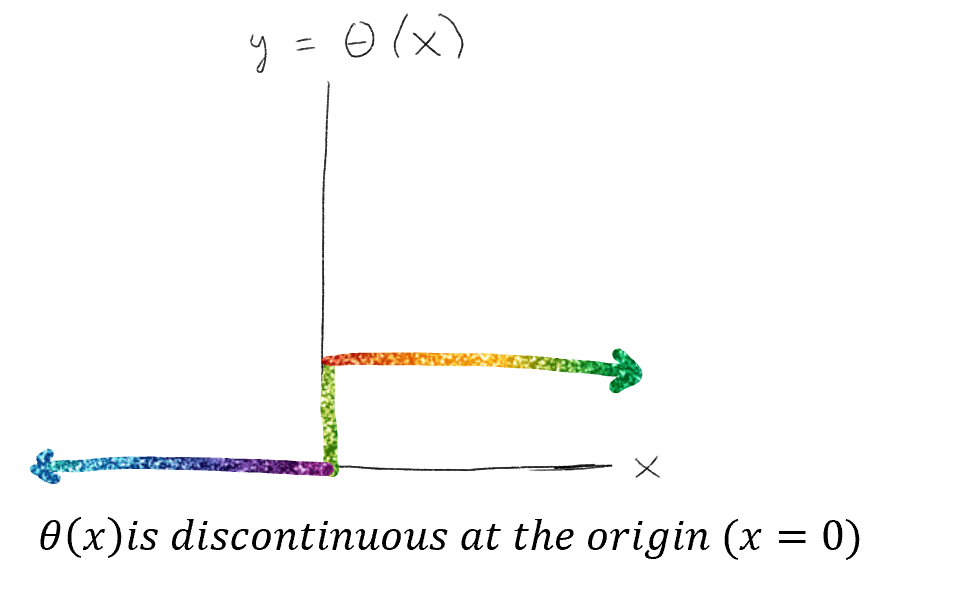
 RSS Feed
RSS Feed