Menu
Substance
A summary of Penrose's summary of physics and math.
|
Fundamental Theorem of Algebra: any polynomial of the form \(a_{0} + a_{1}z + a_{2}z^{2} + a_{3}z^{3} + ... + a_{n}z^{n} = 0\) where \(a_{i}\) are complex numbers and \(a_{n} \ne 0\) will always have a solution.
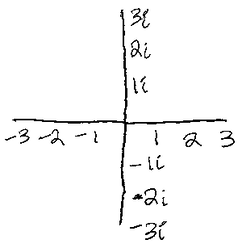
power series = infinite sum of the form \(a_{0} + a_{1}x + a_{2}x^{2} + a_{3}x^{3} + ... = \sum_{i = 0}^{\infty} a_{i}x^{i}\) the number \(z = x + iy\) is represented on the complex plane:
for any power series \(a_{0} + a_{1}z + a_{2}z^{2} + a_{3}z^{3} + ...\) where \(z\) is a complex plane value, there exists a circle of convergence centered at 0 where the series converges for all values inside the circle
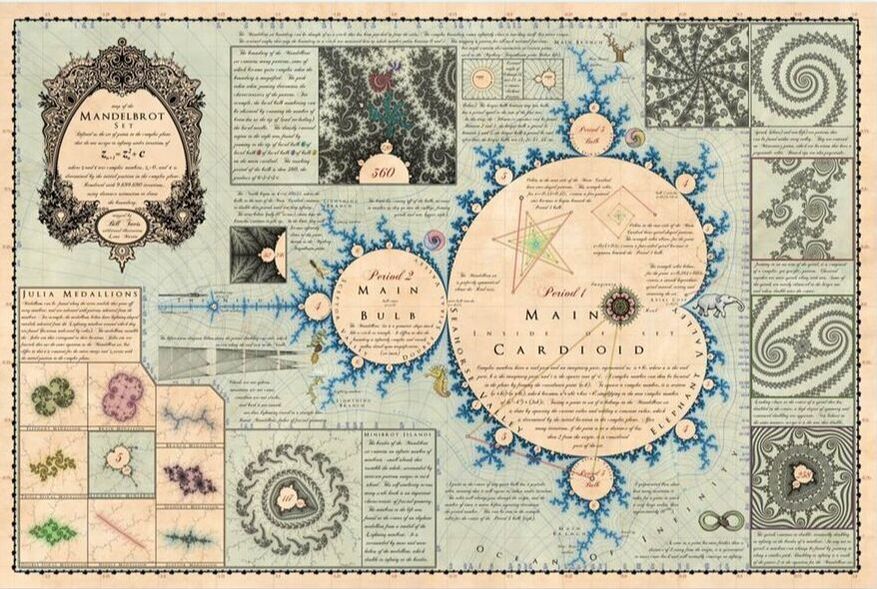
- if radius of convergence = 0, then series diverges for all \(z \ne 0\) - if radius = \(\infty\), series converges for all \(z\) The radius of convergence is determined by the singularity of the series closest to the origin in the complex plane. Poles = singularities of a complex valued power series arising from the vanishing of a polynomial in reciprocal form. The Mandelbrot Set
Let \(c = \) some point in the complex plane
Let \(z = 0\) We iteratively apply the transformation \(z \mapsto z^{2} + c\) for a given \(z\) instance, 1. if \(z\) goes to \(\infty\), then color \(c\) white 2. if \(z\) is confined to a finite region, color \(c\) black So \(z\) is just some starting point, ie., the origin and \(c\) is the location on the complex plane in consideration so a computer would do the above for each \(c\) in the plane. Condition 1 = unbounded sequence Condition 2 = bounded Mandelbrot set = the set of \(c\) values where we have a bounded sequence
0 Comments
Leave a Reply. |
Archives
April 2022
Categories |
 RSS Feed
RSS Feed