Menu
Substance
A summary of Penrose's summary of physics and math.
|
Recall: on a torus there are loops that can be drawn which cannot be continuously deformed down to a single point...this characterizes a torus relative to a sphere (on which all loops can be contracted as described).
Manifolds and Coordinate Patches
"An \(n\)-manifold \(\mathcal{M}\) can be constructed completely analogously to the way in which, in chapters 8 and 10 (sec. 10.2), we constructed the surface \(S\) from a number of coordinate patches" (pg. 221).
\(\bullet\) need \(n\) coordinates in each patch (\(n\) = dimension of \(\mathcal{M}\)) \(\bullet\) in this context, upper number indices distinguish coordinates \(x^{1}\), \(x^{2}\), ..., \(x^{n}\) \(\bullet\) each patch is an open region of \(\mathbb{R}^{n}\), they are glued together to form \(\mathcal{M}\), transition functions express coordinates from one patch in terms of those of another patch \(\bullet\) Hausdorff space = standard type of manifold, for any 2 distinct points of the space, there are open sets containing each which do not intersect \(\bullet\) non-Hausdorff space = can "branch" (interesting) \(\star\star\star\) Scalars, Vectors, and Covectors
Let \(\Phi\) be a smooth function/scalar field on \(\mathcal{M}\). Let \(\mathcal{E}\) be a vector field on \(\mathcal{M}\) which acts on any smooth scalar field \(\Phi\) to produce another scalr field \(\mathcal{E}(\Phi)\) like a differential operator satisfying: \[\mathcal{E}(\Phi + \Psi) = \mathcal{E}(\Phi) + \mathcal{E}(\Psi)\] \[\mathcal{E}(\Phi\Psi) = \Phi\mathcal{E}(\Psi) + \Psi\mathcal{E}(\Phi)\] \[\mathcal{E}(k) = 0 \textrm{ if } k \textrm{ is a constant}\] We can define 1-forms/covector fields algebraically too
\(\bullet\) let \(\alpha\) be a covector field (map from vector feilds to scalar fields) \(\bullet\) \(\alpha\bullet\mathcal{E}\) = action of \(\alpha\) on \(\mathcal{E}\) = scalar product \(\bullet\) for any vector fields \(\mathcal{E}\) and \(\eta\) + scalar field \(\Phi\) we have linearity relations \[\alpha\bullet(\mathcal{E}+\eta) = \alpha\bullet\mathcal{E}+\alpha\bullet\eta\] \[\alpha\bullet(\Phi\mathcal{E}) = \Phi(\alpha\bullet\mathcal{E})\] \(\bullet\) covectors = dual objects to vectors \(\bullet\) the above expressions are symmetrical: \[(\alpha+\beta)\bullet\mathcal{E} = \alpha\bullet\mathcal{E} + \beta\bullet\mathcal{E}\] \[(\Phi\alpha)\bullet\mathcal{E} = \Phi(\alpha\bullet\mathcal{E})\] "Vectors taken at a particular fixed point \(o\) [of \(\mathcal{M}\)] constitute a vector space" (pg. 224). \(\bullet\) Tangent space \(T_{o}\) at point \(o\) of \(\mathcal{M}\) = flat vector space that provides structure of \(\mathcal{M}\) in the immediate neighborhood of \(o\) \(\bullet\) \(T_{o}\) has dimension \(n\) and \(n\) basis elements \(\frac{\partial}{\partial x^{1}}\), \(\frac{\partial}{\partial x^{2}}\), ..., \(\frac{\partial}{\partial x^{n}}\) at the point \(o\) \(\bullet\) cotangent space \(T_{o}^{\star}\) (to \(\mathcal{M}\) at \(o\)) is the dual of \(T_{o}\) Gradient/vector derivative \(d\Phi\) of scalar field \(\Phi\) = example of covector field. \(d\Phi\) is covector with components \(\frac{\partial\Phi}{\partial x^{1}}\), ..., \(\frac{\partial\Phi}{\partial x^{n}}\) has \(d\Phi\bullet\mathcal{E} = \mathcal{E}(\Phi)\) property. The difference between covector and vector? At each point of \(\mathcal{M}\) \(\bullet\) covector \(\alpha = (n - 1)\) dimensional plane element \(\bullet\) directions determined by vectors \(\mathcal{E}\) for which \(\alpha\bullet\mathcal{E} = 0\) (when \(\alpha = d\Phi\), the plane elements are tangential to the family of \((n-1)\)-dimensional surfaces of constant \(\Phi\), thereby generalizing notion of contour lines) "In general the \((n-1)\)-plane elements defined by a covector \(\alpha\) would twist around in a way that prevents then from consistently touching any such family of \((n-1)\)-surfaces" (pg. 225). \(\bullet\) Given coordinate patch with coordinates \(x^{1}\), ..., \(x^{n}\) we have a vector field \(\mathcal{E}\) with components \(\mathcal{E}^{1}\), ..., \(\mathcal{E}^{n}\) ie. \[\mathcal{E} = \mathcal{E}^{1}\frac{\partial}{\partial x^{1}} + \mathcal{E}^{2}\frac{\partial}{\partial x^{2}} + ... + \mathcal{E}^{n}\frac{\partial}{\partial x^{n}}\] \(\bullet\) A covector field \(\alpha\) in the same coordinate patch is represented as \(\alpha = \alpha_{1}dx^{1} + \alpha_{2}dx^{2} + ... + \alpha_{n}dx^{n}\) where \(dx^{1}\), \(dx^{2}\), \(dx^{n}\) are 1-forms. Each \(dx^{r}\) refers to the \((n-1)\)-plane elements spanned by all the coordinate aces with the exception of the \(x^{r}\)-axis." (pg. 227) \(\bullet\) scalar product is then \(\alpha\bullet\mathcal{E} = \alpha_{1}\mathcal{E}^{1} + \alpha_{2}\mathcal{E}^{2} + ... + \alpha_{n}\mathcal{E}^{n}\) Grassmann Products
\(\bullet\) \(\mathcal{E}\wedge\eta\) = 2-plane element at a point of \(\mathcal{M}\) where \(\mathcal{E}\) and \(\eta\) are 2 independent vectors spanning the 2-planes (a bivector) and has components \[\mathcal{E}^{[r}\eta^{s]} = \frac{1}{2}(\mathcal{E}^{r}\eta^{s} - \mathcal{E}^{s}\eta^{r})\]
\(\bullet\) sum \(\psi\) of bivectors \(\mathcal{E}\wedge\eta\) is also a bivector \(\psi\) has components \(\psi^{rs}\) which are antisymmetric \(\psi^{rs} = -\psi^{sr}\) \(\bullet\) \(\mathcal{E}\wedge\eta\wedge\zeta\) = trivector with components given by \[\mathcal{E}^{[r}\eta^{s}\zeta^{t]} = \frac{1}{6}(\mathcal{E}^{r}\eta^{s}\zeta^{t} + \mathcal{E}^{s}\eta^{t}\zeta^{r} + \mathcal{E}^{t}\eta^{r}\zeta^{s} - \mathcal{E}^{r}\eta^{t}\zeta^{s} - \mathcal{E}^{t}\eta^{s}\zeta^{r} - \mathcal{E}^{s}\eta^{r}\zeta^{t})\] ie. = \(\frac{1}{6}(\) sum of \(\mathcal{E}^{r}\eta^{s}\zeta^{t}\) with indices permuted and all odd permutations are negative) \(\bullet\) general trivector \(\tau\) has completely antisymmetric components \(\tau^{rst}\) \(\bullet\) consider \(p\) independent 1-forms \(\alpha\), \(\beta\), ..., \(\delta\) and their wedge product \(\alpha\wedge\beta\wedge...\wedge\delta\) which has components given by \(\alpha_{[r}\beta_{s}...\delta_{u]}\). ---- this is an \((n-p)\)-plane element since \(\mathcal{M}\) has dim. \(n\) and we have \(p\) 1-forms ---- the element is given by the intersection of the \((n-1)\) plane elements of each individual 1-form ---- \(\alpha\wedge\beta\wedge...\wedge\delta\) is a "simple \(p\)-form" \(\bullet\) A \(p\)-form has components represented by \(\psi_{rs...u}\) where each index ranges from 1 to \(n\) and there are \(p\) such subscript indices, they are also antisymmetrical \(\bullet\) The \((p+q)\)-form \(\psi\wedge\chi\) where \(\chi\) is a \(q\)-form has components \(\psi_{[rs...u}\chi_{jk...m]}\) Integrals of Forms
Given \(\int f(x)dx\), we can think of \(f(x)dx\) as a 1-form. "In Cartan's scheme we do not think of '\(dx\)' as denoting an 'infinitesimal quantity,' however, but as providing us with the appropriate kind of density (1-form) that one may integrate over a curve." (pg. 230)
\(\bullet\) Suppose we change the parameter \(\chi\) to \(X\) for the 1-form \(\alpha=f(\chi)d\chi\) ... then \(\alpha\) doesn't change! Ie. \(\int\alpha\) is the same (though its explicit expression is not) so we have the notation \(\int\alpha\) or \(\int_{\mathcal{R}}\alpha\) where \(\mathcal{R}\) = some portion of the given curve \(\gamma\) over which the integral is to be taken \(\bullet\) for an integral over a 2D region we can have \[\int_{\mathcal{R}}f(x, y)dx\wedge dy = \int_{\mathcal{R}}\alpha\] \(\mathcal{R}\) is now a 2D region. Exterior Derivative
Let \(d\) be an operator taking \(p\)-forms to \((p+1)\)-forms with the properties \[d(\alpha+\beta) = d\alpha + d\beta\] \[d(\alpha\wedge\gamma) = d\alpha\wedge\gamma + (-1)^{p}\alpha\wedge d\gamma\] \[d(d\alpha) = 0\] \(\star\star\star\) for the last one, ie. \(d^{2} = 0\)
\(\bullet\) Poincare lemma: if a 1-form \(\alpha\) satisfies \(d\alpha = 0\) then it must locally have the form \(\alpha = d\phi\) by the above properties. More generally, if a \(p\)-form \(\beta\) satisfies \(d\beta = 0\), then locally \(\beta\) has the form \(\beta = d\gamma\) for some \((p-1)\)-form \(\gamma\) Suppose we have a \(p\)-form \(\alpha\) in/on a coordinate patch with coordinates \(x^{1}\), ..., \(x^{n}\) represented as: \[\alpha = \sum\alpha_{r...t}dx^{r}\wedge...\wedge dx^{t}\] where \(\sum\) is over all sets of \(p\) indices \(r\), ..., \(t\) each of which can be an integer from 1 to \(n\) \(\bullet\) exterior derivative of \(\alpha\) is a \((p+1)\)-form \(d\alpha\) with components \[(d\alpha)_{qr...t} = \frac{\partial}{\partial x^{[q}}\alpha_{r...t]}\] \(\bullet\) fundamental theorem of exterior calculus \[\int_{\mathcal{R}}d\psi = \int_{\partial\mathcal{R}}\psi\] where \(\mathcal{R}\) is a compact \((p+1)\) dimensional oriented region with oriented \(p\) dimensional boundary denoted by \(\partial\mathcal{R}\). Volume Elements; Summation Convention
Consider \(n\)-form \(\epsilon\) on an \(n\)-dim manifold \(\mathcal{M}\)
---- associated \(n\)-surface element at point \(o\) of \(\mathcal{M}\) is the entire tangent \(n\)-plane at \(o\) ---- \(\epsilon\) gives measure that is an \(n\)-density (with no directional properties) often called a volume element \(\bullet\) vol element can be used to convert \((n-p)\) vectors to \(p\) forms and vice versa \(\bullet\) for an \(n\)-form \(\epsilon\) with components \(\epsilon_{r...w}\) and an \((n-p)\)-vector \(\psi\) with components \(\psi^{u..w}\)....tensor contraction is defined as follows: glue the \(n-p\) upper indices of \(\psi^{u..w}\) to the \(n-p\) lower indices of \(\epsilon_{r...w}\), leaving \(p\) indices for \(\alpha_{r...t}\) which is a component of a \(p\)-form Example of tensor contraction is the scalar product \(\bullet\) for covector \(\beta\) with components \(\beta_{r}\) \(\bullet\) \(\xi\) vector with components \(\xi^{r}\) \(\rightarrow\) multiply corresponding elements of both sets of components together and then sum over repeated indices to get \[\beta\bullet\xi = \sum\beta_{r}\xi^{r}\] \(\bullet\) Summation Convention: the omission of actual summation sign + assumption that summation is taking place whenever the same index letter appears in both the lower and upper positions in a term. Tensors: Abstract-Index and Diagrammatic Notation
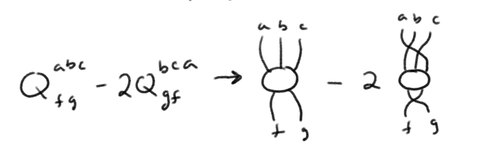
A tensor is denoted as \(Q_{a..c}^{f..h}\) which has \(q\) lower and \(p\) upper indices for \(p\), \(q \geq 0\) and does not necessarily have any special symmetries.
\(\bullet\) This a \((p, q)\)-valent tensor or just a \((p, q)\)-tensor or a tensor of valence \((p, q)\) (this is not the notation used in book but idk how to get the correct one) \(\bullet\) represents a multilinear function \(Q\) of \(q\) vectors \(A\), ..., \(c\) and \(p\) covectors \(F\), ..., \(H\) \[Q(A...C;F...H) = A^{a}...C^{c}Q_{a..c}^{f..h}F_{f}..H_{h}\] \(\bullet\) In diagrammatic notation the tensor \(Q\) is some symbol with \(q\) lines extending downward and \(p\) lines extending upwards. \(\bullet\) For any two indices that are contracted together, the lines must be connected, upper to lower
See pages 241 and 242 for other examples.
\(\star\) A bar is drawn scross index lines to denote antisymmetrization. \(\star\) A wiggly bar mirrors symmetrization. Complex Manifolds
\(\bullet\) Now have complex coordinates \(z^{1}\), ..., \(z^{n}\) characterizing the coordinate patches
\(\bullet\) Transition funitions between coordinate patches must be holomorphic functions. \(\bullet\) Should we instead express all \(z^{i}\) terms in terms of their real and imaginary parts as \(z^{i} = x^{i} + iy^{i}\), then the complex \(n\)-manifold becomes a real \(2n\)-manifold with complex local structure. \(\bullet\) For real vector fields \(\xi\) and \(\eta\), we can define a complex vector field as \(\zeta = \xi + i\eta\). \(\bullet\) By the Newlander-Nirenberg theorem, if a differential equation in the quantity \(J\) (where \(J(\xi) = -\eta\) and \(J(\eta) = \xi\) and \(J^{2} = -1\)) is satisfied, then a \(2n\) dimensional real manifold, with \(J\) structure, can be reinterpreted as a complex \(n\)-manifold.
0 Comments
Leave a Reply. |
Archives
April 2022
Categories |
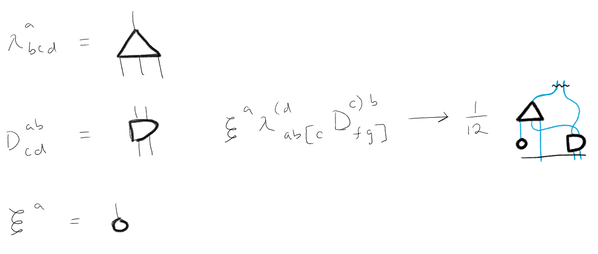
 RSS Feed
RSS Feed