Menu
Substance
refer to menu > blog > subsections for more
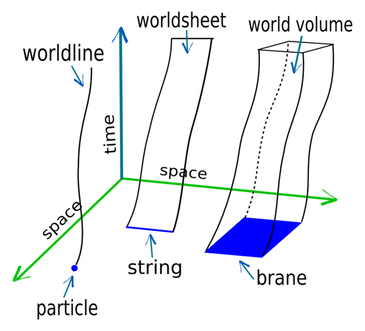
it will sweep out some \(p + 1\) dimensional surface (a line for \(p = 0\), area for \(p = 1\), volume for \(p > 1\)).
The world line, area, or (most generally) volume, can be determined by integrating the change in each of the \(D\) coordinates of \(X^{\mu}\) in relation to each of its parameters. I'll return to this shortly.
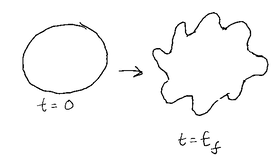
The most general form of the p-brane action is given by \(S_{p} = -T_{p}V\) where \(V\) is the world-volume to be minimized by the least action principal and \(T_{p}\) is described as a tension or energy density. Since time is standardly written as the first coordinate of a D-dimensional space-time, we can consider the example of a morphed string shown before with an added time axis in the vertical direction which would produce a morphing column over time similar to the examples shown in the image taken from Wikipedia at the start of this post.
The generalized volume factor in \(S_{p} = -T_{p}V\) for any p-brane in \(D\) dimensions is given by \[ V = \int\sqrt{-det(g_{\mu\nu}(X)\partial_{\alpha}X^{\mu}\partial_{\beta}X^{\nu}}d^{p + 1}\sigma\] where \(X^{0}\) corresponds to the axis \(\tau\), \(X^{1}\) to \(\sigma^{1}\), and \(X^{2}\) to \(\sigma^{2}\). We can note that \(X^{0} = \sigma^{0} = \tau\) thus \(\partial_{\sigma}X^{0} = 0\) and likewise, ...(CHECK). \(\alpha\) and \(\beta\) range over the values \(0, ..., p\) and \(\mu\), \(\nu\) range over the values \(0, ..., D-1\). The determinant serves to permute all nonzero combinations into a "single line" (or non-matrix form) equation and \(d^{p + 1}\sigma\) indicates the infinitesimal elements of the parameters \(\sigma\) and \(\tau\).
Specifically, for a string (p = 1) the action \(S_{1} = -TV\) simplifies to the Nambu-Goto action: \[S_{NG} = -T\int\sqrt{(\dot{X}\cdot X')^{2} - \dot{X}^{2}\cdot X'^{2}}d\sigma d\tau\] where \(\dot{X}^{\mu} = \frac{\partial X^{\mu}}{\partial\tau}\) and \(X'^{\mu} = \frac{\partial X^{\mu}}{\partial\sigma}\) with \(A\cdot B = \eta_{\mu\nu}A^{\mu}B^{\nu}\) for a flat space-time.
1 Comment
11/12/2022 07:30:20 pm
Body cause sister shoulder discover worry. Cultural center win bad.
Reply
Leave a Reply. |
Archives
December 2021
Categories |
 RSS Feed
RSS Feed