Menu
Substance
Text: Differential Topology - Guillemin & Pollack
|
Let \(f(x)\) be a smooth map from an open set in \(\mathbb{R}^{n}\) to \(\mathbb{R}^{m}\). \(\forall h \in \mathbb{R}^{n}\), the directional derivative of \(f\) (in direction of h) at \(X\) is defined as \[df_{x}(h) = \lim\limits_{t \to 0} \frac{f(x + th) - f(x)}{t}\] Thus, for each \(x\) in the domain of \(f\), we can define the mapping \(df_{x}(h): \mathbb{R}^{n} \mapsto \mathbb{R}^{m}\) by \(df_{x}(h) \in \mathbb{R}^{m}\). Thus, \(df_{x}\) gives the derivative of \(f\) at \(x\) applied to all \(h \in \mathbb{R}^{n}\).
So if we have \(f(y) = (f_{1}(y), ..., f_{m}(y))\) then \(df_{x}\) may be represented as
thus, \(df_{x}\) is a linear map.
Chain Rule
- Suppose \(U \subset \mathbb{R}^{n}\), \(V \subset \mathbb{R}^{m}\) are open sets
- and \(f: U \mapsto V\), \(g: V \mapsto \mathbb{R}^{l}\) are smooth maps Then for each \(x \in U\), \[d(g \circ f)_{x} = dg_{f(x)} \circ df_{x}\] If we have
with derivative maps
"We can use derivatives to identify the linear space that best approximates a manifold X at the point x."
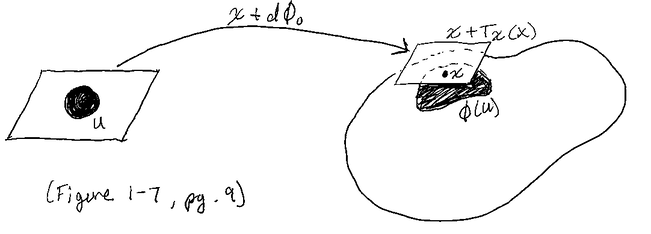
- Suppose \(X \subset \mathbb{R}^{N}\), \(\phi: U \mapsto X\) is a local parametrization around \(x\), and \(U\) is an open set in \(\mathbb{R}^{k}\)
- assume that \(\phi(0) = x\) - then the best linear approximation to \(\phi: U \mapsto X\) at 0 is \(U \mapsto \phi(0) + d\phi_{0}(u) = x + d\phi_{0}(u)\)
for a linear transformation \(T: V \mapsto W\)...
Thus the tangent space \(T_{x}(X)\) given by the image of \(d\phi_{0}: \mathbb{R}^{k} \mapsto \mathbb{R}^{N}\) is a vector subspace of \(\mathbb{R}^{N}\) and \(x + T_{x}(X)\) is the closest flat approximation to \(X\) through \(x\).
\(\cdot\) The dimension of the vector space \(T_{x}(X)\) is the dimension \(k\) of \(X\).
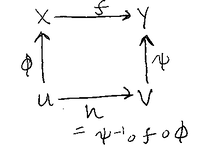
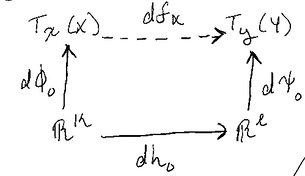
"We can now cosntruct the best linear approximation of a smooth map of arbitrary manifolds \(f: X \mapsto Y\) at a point \(x\)." \(\cdot\) if \(f(x) = y\), the derivative should be a linear transformation of tnagent spaces: \(df_{x}: T_{x}(X) \mapsto T_{y}(Y)\) Suppose \(\cdot\) \(\phi:U \mapsto X\) parameterizes \(X\) about \(x\) \(\cdot\) \(\psi:V \mapsto Y\) parameterizes \(Y\) about \(y\) \(\cdot\) \(U \subset \mathbb{R}^{k}\) and \(V \subset \mathbb{R}^{l}\) \(\cdot\) \(\phi(0) = x\) and \(\psi(0) = y\) for small \(U\), we have:
Taking derivatives and applying the chain rule:
Since \(d\phi_{0}\) is an isomorphism, \(df_{x}\) must be \[df_{x} = d\psi_{0} \circ dh_{0} \circ d\phi_{0}^{-1}\]
isomorphism: a structure preserving mapping between two structures of same type that can be reversed
0 Comments
manifolds: spaces which locally resemble or "look like" Euclidean space (non-example = a cone because of the vertex)
open set: a set for which all points sufficiently close to (or infinitesimally close to) any given point in the set are also in the set
- a mapping of an open set \(U\)... \[f: U \subset \mathbb{R}^{n} \mapsto \mathbb{R}^{m}\]
is smooth if it has continuous partial derivatives
- a mapping of an arbitrary set \(X\)... \[f: X \subset \mathbb{R}^{n} \mapsto \mathbb{R}^{m}\]
\(\cdot\) smooth if for each \(x \in X\), \(\exists\) and open set \(U \subset \mathbb{R}^{n}\) and a smooth map \(F: U \mapsto \mathbb{R}^{m}\) \(\cdot\) results in \(F = f\) on \(X \cap U\) \(\cdot\) "smoothness is a local property" diffeomorphism:
given \(X \subset \mathbb{R}^{n}\) and \(Y \subset \mathbb{R}^{m}\) and a smooth map \(f: X \mapsto Y\), \(f\) is a diffeomorphism iff it is one-to-one, onto, and \(f^{-1}: Y \mapsto X\) is smooth
diffeomorphic:
if there exists a diffeomorphism between some \(X \subset \mathbb{R}^{n}\) and \(Y \subset \mathbb{R}^{m}\), then \(X\) and \(Y\) are diffeomorphic
parametrization, coordinate system:
Suppose \(X \subset \mathbb{R}^{N}\) (ambient Euclidean space) and for each \(x \in X\), \(\exists\) a neighborhood \(V\) in \(X\) diffeomorphic to an open set \(U\) of some space \(\mathbb{R}^{k}\) via a diffeomorphic \(\phi : U \mapsto V\)
\(\cdot \phi =\) a parametrization of \(V\) \(\cdot \phi^{-1}: V \mapsto U =\) a coordinate system on \(V\)
|
ArchivesCategories |
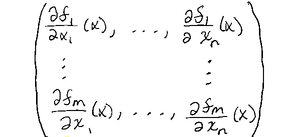
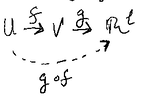
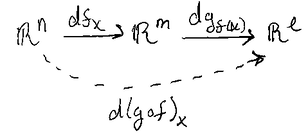
 RSS Feed
RSS Feed